群体结构分析三种常用方法 (上篇) | Universe Biology Girls and Boys

Bioinformatics

Publish Date: 2019-05-13

Word Count: 1.9k

Read Times: 7 Min

Read Count:

写在前面

在群体遗传学和进化生物学相关的项目中，群体结构分析是最常见也是最初步的分析内容，可以帮助我们确认样本分群是否符合预期以及检测离群样本。群体结构分析最常用的三种方法就是PCA、系统发生树和祖先成分堆叠图，下面我们将使用发表在Genome Rearch上的Gou et al,2014中的数据（60只狗全基因组SNP）逐一讲解。

一、 PCA分析

1. 简单介绍PCA原理

PCA (Principal Component Analysis) ，即主成分分析方法，是一种使用最广泛的数据降维算法，通过正交变换将一组数量庞大且可能存在相关性的变量转换为一组低维的线性不相关的变量。
对于一个全基因组测序样本call出的SNP数目通常是百万级甚至是千万级别，比如本文所用数据为17M SNP，如果直接使用这些SNP位点作为指标对个体进行区分，就会由于信息过于冗杂而无法把握重点，并造成计算资源和时间的浪费。PCA分析的过程就是从千万级别的SNP位点中提取关键信息，以便我们使用更少的变量就可以对样本进行有效的刻画和区分。

2. PCA实践

在Gou et al, 2014文章中，作者使用GCTA进行PCA分析，在本文中，还会讲解另外一种主流的PCA分析软件–EIGENSOFT中的smartpca。

软件下载链接：
GCTA
EIGENSOFT

GCTA进行PCA分析

首先准备GCTA中PCA模块所需的输入文件，GCTA可以直接读取.bed , .bim , .fam文件，使用plink将vcf格式文件转换成上述三种文件,同时进行简单的过滤(–geno 0.05)。

#!/bin/bash

plink=/software/biosoft/software/plink/plink
time $plink --vcf 60_dog.merge.vcf --geno 0.05 --dog --make-bed --out 60_dog_geno0.05 && echo "---- vcf2bed done -----"

然后使用GCTA软件，–make-grm 生成个体对之间的遗传关系矩阵(genetic relationship matrix),并将GRM的下三角元素保存为二进制文件.grm.id , .grm.bin ， .grm.N.bin。
这里要强调一点，对于非人物种，要设定好染色体数目参数，–autosome-num。否则会因为不识别26以上的染色体编号而报错。

gcta=/software/biosoft/software/gcta_1.92.1beta6/gcta64
time $gcta --bfile 60_dog_geno0.05 --make-grm --autosome-num 38 --out 60_dog_geno0.05 && echo "----make-grm done----"

最后就是要进行PCA分析
使用 –pca 设置要生成主成分的数目，这里设置为4，一般来说就可以刻画出群体结构。
这一步会生成 .eigenval 和 .eigenvec 两个文件。.eigenval文件为各主成分可解释遗传信息的比例，.eigenvec文件为每个样本在top4主成分上的分解值。

time $gcta --grm 60_dog_geno0.05 --pca 4 --out 60_dog_geno0.05 && echo "----gcta-pca done----"

补充样本所属子群信息
在生成的.eigenvec文件中，并没有包含样本所属子群信息，在进行可视化之前，需要添加上样本群体信息。样本较少时可以手动添加，样本数目较多时推荐写代码完成，避免错误。文章Gou et al,2014中根据采样地点划分子群。添加上子群信息后，.eigenvec长这个样子。
EIGENSOFT进行PCA分析
使用plink将vcf格式文件转换成.bed , .bim , .fam文件，步骤同上，这里不再赘述。
smartpca需要提供三种输入文件，文件1记录每个样本在每个SNP位点的信息，文件2记录每个SNP位点的信息，文件3记录每个样本的性别和所属子群信息。
熟悉plink格式的同学应该知道.bed文件储存的就是genotype信息，.bim文件存储的就是SNP位点信息，那么我们只需要自己生成文件3就可以了。文件3格式如下，第一列为样本ID，第二列为性别（M，F，U），第三列为所属子群。
接下来把所有参数写入一个文件中，就可以运行smartpca了，其中 numoutevec 是输出主成分的数目。
运行smartpca，生成 .evec 和 .eval 文件。
```
time /software/biosoft/software/EIG-6.1.4/bin/smartpca -p PCA.par > smartpca.log && echo "----smartpca----done"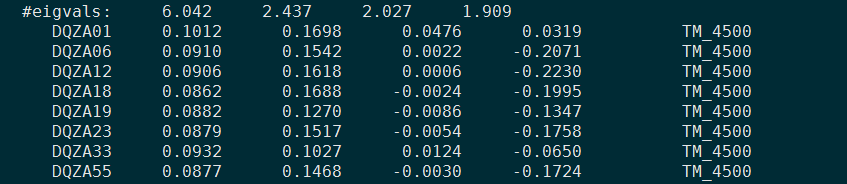
```
截图来看下 .evec 文件，两种软件运行结果差不多。

3. 绘制PCA散点图

通过得到的.evec和eval两个文件，这里使用python完成可视化，代码如下：

import matplotlib.pyplot as plt
import collections
import re

hash = collections.OrderedDict()
eval_file = open("60_dog_geno0.05.eigenval","r")
evec_file = open("60_dog_geno0.05.eigenvec","r")

###  从.eval文件中读取top4主成分
eval_1 = eval_file.readline()
eval_2 = eval_file.readline()
eval_3 = eval_file.readline()
eval_4 = eval_file.readline()


###  从.evec文件中读取在pc上的值
for i in evec_file:
    if re.match(r'#',i.strip()):
        continue
    tmp = i.strip().split()[1:]
    if tmp[-1] in hash.keys():
        hash[tmp[-1]]['1st'].append(eval(tmp[1]))
        hash[tmp[-1]]['2nd'].append(eval(tmp[2]))
        hash[tmp[-1]]['3rd'].append(eval(tmp[3]))
        hash[tmp[-1]]['4th'].append(eval(tmp[4]))
    else:
        hash[tmp[-1]] = hash.get(tmp[-1],collections.OrderedDict())
        hash[tmp[-1]]['1st'] = hash[tmp[-1]].get('1st',[])
        hash[tmp[-1]]['2nd'] = hash[tmp[-1]].get('2nd',[])
        hash[tmp[-1]]['3rd'] = hash[tmp[-1]].get('3rd',[])
        hash[tmp[-1]]['4th'] = hash[tmp[-1]].get('4th',[])
        hash[tmp[-1]]['1st'].append(eval(tmp[1]))
        hash[tmp[-1]]['2nd'].append(eval(tmp[2]))
        hash[tmp[-1]]['3rd'].append(eval(tmp[3]))
        hash[tmp[-1]]['4th'].append(eval(tmp[4]))

### 绘制散点图，这里只绘制pc1和pc2,其他pc可按照下面代码逐一画出。
fig = plt.figure(figsize=(20,10))
ax = fig.add_subplot(1, 1, 1)            ### 2D figure
#ax = fig.add_subplot(111,projection='3d')              ### 3D figure
mark = ['o','v','s','*','x','+']*10         ### 设置散点性状
col = ['b','g','y','r','c']*10               ### 设置散点颜色
for m,n in enumerate(hash.keys()):    ### 逐点画出
    ax.scatter(hash[n]['1st'],hash[n]['2nd'],c=col[m],s=75,marker=mark[m],label=n,alpha=0.7)
ax.legend(loc='best',scatterpoints=1,fontsize='12',framealpha=0)
ax.set_xlabel('Eigenvector1 ({}%)'.format(float('%.2f' % eval(eval_1))),fontsize=13,fontweight='bold')
ax.set_ylabel('Eigenvector2 ({}%)'.format(float('%.2f' % eval(eval_2))),fontsize=13,fontweight='bold')

#### 保存图片
save_FileName = '60dog_geno0.05_gcta_pc1_pc2.png'
plt.savefig(save_FileName,dpi=400,bbox_inches='tight')

PCA散点图如下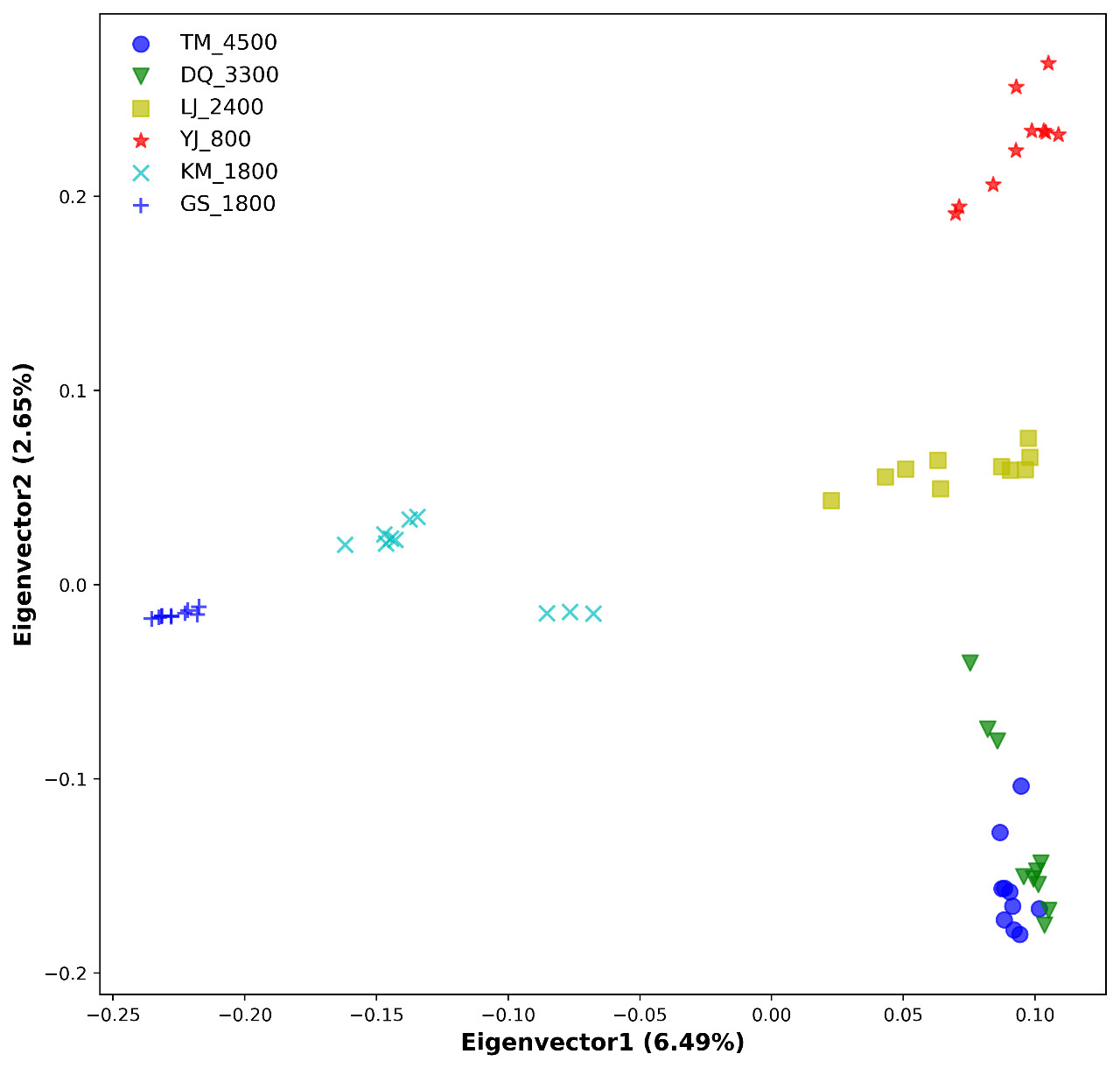
#### 小结
PCA运用方差分解，将海量SNP的差异反映在二维坐标图上，坐标轴轴取对样品差异性解释度最高的两个或三个特征值，样本SNP位点信息越相似，反映在PCA图中的距离越近。PCA可以帮助我们清楚掌握手上样本的群体结构，并有效检测出离群样本，为下游分析减少不必要的麻烦，同时，实现PCA分析的方法很多，PCA结果图也简单易懂，称得上是低调实力派。
最后强调一点，PCA分析是降维，不是聚类，希望大家不要搞混了。
对PCA理论和分析过程感兴趣的同学，可以进一步看下这篇文章。