R语言编程入门

写在前面的

上期推文介绍了如何使用R语言编程进行样本间相关性分析，主要涉及了R语言矩阵、循环、统计分析函数、ggplot2、corrplot等函数包的使用，涉及的知识面较多，如果不是经常做生物信息或者是编程出家，很难在短时间内适应编程模式。其实，一旦适应了编程，很多问题都能轻松迎刃而解。毕竟计算机语言也是一门语言，和人与人之间打交道一样，人与计算机打交道也是很容易的。本次推文以引导大家入门R语言编程为目的，用尽可能精炼的内容教学R语言。认识R语言首先认识R语言的数据类型及控制结构。掌握这些基础以后，再认识R语言的函数包。经过一定时间的练习就可以熟悉R语言了。

R语言数据类型1：向量

向量是R语言最基本的数据类型。R语言中向量和大学时候学的线性代数一样，是由一行或者一列数据组成的变量。

x<-c(1,2,3,4,5) #把向量赋值给x，c是连接函数。此时x就是由数字1到5组成的向量
length(x) #获取向量长度
x[3]#x的第三个元素
x[-1:-2] #删除x前两个元素
x<-x[-1:-2] #删除x前两个元素并保存
b<-seq(from=1,to=100,by=2) #seq是生成等差数列函数，from是数列起始值to是终止值，by是公差

R语言数据类型2：矩阵

R语言矩阵可以理解为多个长度相同的向量按照行或列排列而成的多维向量，R语言矩阵与线性代数中的矩阵稍有不同，不同点在于矩阵的乘法计算上，线性代数中矩阵乘法计算方法为设A为 mxp 的矩阵，B为 pxn 的矩阵，那么称 mxn 的矩阵C为矩阵A与B的乘积,其中矩阵C中的第 i行第 j列元素可以表示为

$$AB_{ij}=\sum_{k=1}^p a_{ik}b_{kj}=a_{i1}b_{1j}+a_{i2}b_{2j}+…+a_{ip}b_{pj}$$

但是R语言中矩阵乘法是对应元素做乘积。举例为

f<-cbind(c(1,2,3),c(4,5,6)) #将两个向量按列捆绑可得得到矩阵,如果想按照行向量捆绑为矩阵用rbind函数
z<-cbind(c(1,2,3),c(4,5,6))
f*z
 [,1] [,2]
[1,]    1   16
[2,]    4   25
[3,]    9   36
x<-matrix(c(1,2,3,4,5,6),ncol=2,nrow=3)#另外一种矩阵赋值方式，ncol定义矩阵的列数，nrow定义矩阵行数，另外ncol(x)或者nrow(x)则可以求矩阵的列数或行数。
x[1,2]#查看矩阵第1行第2列元素,当然如果想查看矩阵第一行则为x[1,]查看第二列为x[,2]。

R语言数据类型3：列表

列表是一种特殊的向量，不同之前的向量。之前的向量可以理解为原子型，列表中可以保存为不同格式的数据。可以是字符串型、数值型等。举例为

j<-list(name="joe",salary=55000,union=T)#其中name，salary，union理解为列表的标签，等号后面的量理解为列表标签的值，可以一个标签对应多个值，但是列表的标签具有唯一性！

Names(j)#获取列表的所有标签。当然如果想使用其他方法查询列表第2个标签可以使用就j$salary，j[2]，或者j[[2]]。两者的区别读者可以通过实践发现。

R语言数据类型4：数据框

数据框与矩阵有很多相似之处，很多矩阵适用的函数数据框同样适用。与矩阵不同的是，数据框里面的数据类型可以不一致，但矩阵维数必须相等，即各列数据长度相等。以一个实例简单介绍数据框

a<-c("apple","pen")
b<-c(17,14)
c<-data.frame(a,b,stringsAsFactors = F) #创建一个简单的数据框，由于矩阵所用的函数多数都适应于数据框，所以这里不再详细介绍。具体操作读者们可以自行在R语言上实践。

R语言数据类型5：因子

因子在实际的数据分析中用到的场合不多。在R语言中，因子（factor）表示的是一个符号一个编号或者一个等级。以一个实际例子让读者理解因子。

x<-c(100,1,4,9,1320)
x<-factor(x) #对向量X进行因子化处理
[1] 100  1    4    9    1320
Levels: 1 4 9 100 1320

从例子中可以看出，因子实际是为向量数据中的每一个元素赋予一个级别。例如元素100，它对应的level是100，比第二个元素1对应的level大，所以在level的排序上，100在第三个level上。

R语言控制结构

常用的两种控制结构为判断和循环，简单地说掌握了基本控制结构和R语言的数据类型是可以进行数据分析的，毕竟任何一种编程语言只要掌握了语法，剩下的就看个人的数学与逻辑素养了。

1.判断结构：通常为if（条件）{命令}else{命令}类型，也有if…else if…else。也可以只有一个if。举例介绍判断结构语法，输入一个数，如果它大于等于10，输出Y，如果大于等于5小于10输出T，否则输出N

x<-6
if(x>=10){print("Y")}else if(x<10 && x>=5){print("T")}else{print("N")}

2.循环结构：R语言中for循环使用较多，通常结构为for(条件){命令}。以简单例子举例for循环语法，定义一个数值向量，将向量中每个元素的平方赋值给新向量。

x<-c(1:9)
y<-NULL
for (i in 1:length(x)) {
   y<-c(y,(x[i])^2)
}
print(y)
[1]  1  4  9 16 25 36 49 64 81

综合运用R语言编程

以上是R语言编程入门最基本的语法，只有逐渐熟悉这些语法，才可以更进一步使用R语言，下面以上次推文的数据为例子，为大家讲一下如何综合运用R语言知识。上次的推文中是利用RNA-seq的reads count数据计算样本间的重复性分析。另外小明师兄的上篇推文RNA-seq中的那些统计学问题(一)为什么是负二项分布，这篇推文从统计学角度出发推理论证了RNA-seq的reads count数据为什么符合负二项分布，下面我们从R语言编程开始利用实际RNA-seq的readscount数据证明一下为什么是负二项分布

根据负二项分布的性质，均值和方差为
$$\mu={pr}/{(1-p)}$$
$$\sigma^2={pr}/(1-p)^2$$
将P用U表示并带入方差表达式得到

$$\sigma^2=\mu^2/r+\mu$$
根据数学知识可以看出方差是均值的二次函数。所以我们这次综合利用R语言编程的知识进行证明。

readcount<-read.table("readscount.txt",header=t,sep="\t") #读取readscout数据 readcount<-readcount[,2:4]#由于第2到4列是一个处理的三个生物学重复，所以就以这三个生物重复的readscount值进行分析 readcount<-readcount[rowsums(readcount)>1,] #过滤掉全为0的行
x<-null #先定义储存每个基因表达均值的变量 y<-null #定义储存每个基因表达方差的变量 for (i in 1:nrow(readcount)) { x<-c(x,mean(as.numeric(readcount[i,]))) #在循环中依次求每个基因表达的均值，并赋值到x向量中 y<-c(y,var(as.numeric(readcount[i,]))) #在循环中依次求每个基因表达的方差，并赋值到y向量中 } data<-data.frame(x="x,y=y)" #将x和y捆绑为数据框 a<-quantile(data[,1],c(0.25,0.75),na.rm="T)" #求基因表达均值的分位数，quantile函数是求分位数函数，na.rm="T是移除NA值，这里的目的是去除掉太大或者太小的数据" b<-quantile(data[,2],c(0.25,0.75),na.rm="T)#求基因表达方差的分位数" data<-data[data[,1]<="as.numeric(a[2])" && data[,1]>=as.numeric(a[1]),]#将data数据框中的基因表达均值列满足在25%~75%分位数之间的行保留
data<-data[data[,2]<=as.numeric(b[2]) && data[,2]>=as.numeric(b[1]),]#将data数据框中的基因表达方差列满足在25%~75%分位数之间的行保留
ggplot(data = data2,aes(x=x,y=y))+geom_point()+geom_smooth(method = "gam",formula=y~poly(x,2)) #使用ggplot2绘制均值-方差散点图，并进行拟合，拟合方法为平滑曲线拟合

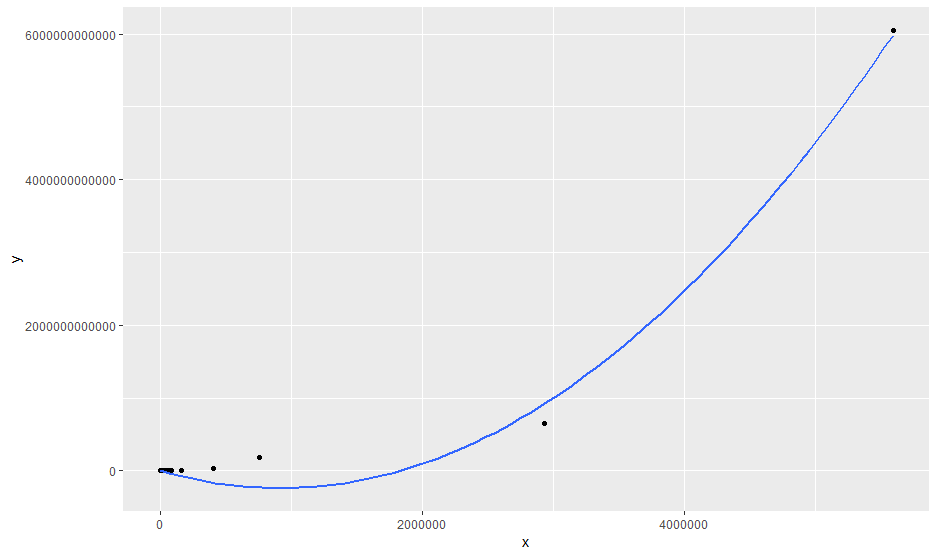
从图片中看出，尽管过滤掉部分数据后还是存在个别极端数据，总体的数据分布曲线满足二次函数分布。