按照惯例,先来个自我介绍:
大家好,我是实习6年的生信狗小明同学,不会唱、跳、Rap,喜欢装X,瞎逼逼和开车(话说我驾照都没啊),以后我将在这里给大家带来生信、统计学和机器学习方面的分享,希望大家能够喜欢(欢呼声和掌声现在可以起来了╭(●`∀´●)╯)
最后给大家提供一个关注我的传送门:
https://ming-lian.github.io,第一时间的更新在我的个人主页上,发到这里的都是在个人主页基础上的整理爱你们哟。:.゚ヽ(。◕‿◕。)ノ゚.:。+゚
下面是正文
1. 多重假设检验的必要性
统计学中的假设检验的基本思路是:
设立零假设(null hypothesis)$H_0$,以及与零假设$H_0$相对应的非零假设(alternative hypothesis, or reject null hypothesis)$H_1$,在假设$H_0$成立的前提下,计算出$H_0$发生的概率,若$H_0$的发生概率很低,基于小概率事件几乎不可能发生,所以可以拒绝零假设
但是这些传统的假设检验方法研究的对象,都是一次试验
在一次试验中(注意:是一次试验, 即single test),0.05 或0.01的cutoff足够严格了(想象一下,一个口袋有100个球,95个白的,5个红的, 只让你摸一次,你能摸到红的可能性是多大?)
但是对于多次试验,又称多重假设检验,再使用p值是不恰当的,下面来分析一下为什么:
大家都知道墨菲定律:如果事情有变坏的可能,不管这种可能性有多小,它总会发生
用统计的语言去描述墨菲定律:
在数理统计中,有一条重要的统计规律:假设某意外事件在一次实验(活动)中发生的概率为p(p>0),则在n次实验(活动)中至少有一次发生的概率为 $p_n=1-(1-p)^n$
由此可见,无论概率p多么小(即小概率事件),当n越来越大时,$p_n$越来越接近1
这和我们的一句俗语非常吻合:常在河边走,哪有不湿鞋;夜路走多了,总能碰见鬼
在多重假设检验中,我们一般关注的不再是每一次假设检验的准确性,而是控制在作出的多个统计推断中犯错误的概率,即False Discover Rate(FDR),这对于医院的诊断情景下尤其重要:
假如有一种诊断艾滋病(AIDS)的试剂,试验验证其准确性为99%(每100次诊断就有一次false positive)。对于一个被检测的人(single test))来说,这种准确性够了;但对于医院 (multiple test))来说,这种准确性远远不够
因为每诊断10 000个个体,就会有100个人被误诊为艾滋病(AIDS),每一个误诊就意味着一个潜在的医疗事故和医疗纠纷,对于一些大型医院,一两个月的某一项诊断的接诊数就能达到这个级别,如果按照这个误诊率,医院恐怕得关门,所以医院需要严格控制误诊的数量,宁可错杀一万也不能放过一个,因为把一个没病的病人误判为有病,总比把一个有病的病人误判为没病更保险一些
100 independent genes. (We have 100 hypotheses to test)
No significant differences in gene expression between 2 classes (H0 is true). Thus, the probability that a particular test (say, for gene 1) is declared significant at level 0.05 is exactly 0.05. (Probability of reject H0 in one test if H0 is true = 0.05)
However, the probability of declaring at least one of the 100 hypotheses false (i.e. rejecting at least one, or finding at least one result significant) is:
$$1-(1-0.05)^{100}\approx 0.994$$
2. 区别p值和q值
|
$H_0$ is true | $H_1$ is true | Total |
|---|---|---|---|
| Not Significant | TN | FN | TN+FN |
| Significant | FP | TP | FP+TP |
| Total | TN+FP | FN+TP | m |
首先从上面的混淆矩阵来展示p值域q值的计算公式,就可以看出它们之间的区别:
p值
p值实际上就是false positive rate(FPR,假正率):
$$p-value=FPR=\frac{FP}{FP+TN}$$
直观来看,p值是用上面混淆矩阵的第一列算出来的
q值
q值实际上就是false discovery rate (FDR):
$$q-value=FDR=\frac{FP}{FP+TP}$$
直观来看,q值是用上面混淆矩阵的第二行算出来的
但是仅仅知道它俩的计算公式的差别还不够,我们还有必要搞清楚一个问题:它俩在统计学意义上有什么不同呢?
p值衡量的是一个原本应该是$H_0$的判断被错误认为是$H_1 \, (reject H_0)$的比例,所以它是针对单次统计推断的一个置信度评估;
q值衡量的是在进行多次统计推断后,在所有被判定为显著性的结果里,有多大比例是误判的
据此,我们可以推导出p值域q值(q值有两种定义,FWER或FDR,这里指的是FWER)之间的关系:
总共有n个features(可以是基因,GWAS中的snp位点等),对它们执行n重假设假设检验后,得到各自对应的p值分别为$\{p^{(i)} \mid i=1,2,…,n\}$
当p值显著性水平取$\alpha$时,得到$k$个features具有p值显著性,它们的p值为$\{p^{(i)}{(j)} \mid j=1,2,…,k\}$,其中$p^{(i)}{(j)}$表示第i个feature它的p值在升序中的排名为j,那么这k个features的FWER可以表示为:
$$FWER=1-\prod_{j=1}^{k}(1-p^{(i)}_{(j)})$$
3. 如何计算q值?
统计检验的混淆矩阵:
|
$H_0$ is true | $H_1$ is true | Total |
|---|---|---|---|
| Significant | V | S | R |
| Not Significant | U | T | m-R |
| Total | m0 | m-m0 | m |
FWER (Family Wise Error Rate)
作出一个或多个假阳性判断的概率
$$FWER=Pr(V\ge 1)$$
使用这种方法的统计学过程:
- The Bonferroni procedure
- Tukey’s procedure
- Holm’s step-down procedure
FDR (False Discovery Rate)
在所有的单检验中作出假阳性判断比例的期望
$$FDR=E\left[\frac{V}{R}\right]$$
使用这种方法的统计学过程:
- Benjamini–Hochberg procedure
- Benjamini–Hochberg–Yekutieli procedure
3.1. Benjamini-Hochberg procedure (BH)
对于m个独立的假设检验,它们的P-value分别为:$p_i,i=1,2,…,m$
(1)按照升序的方法对这些P-value进行排序,得到:
$$p_{(1)} \le p_{(2)} \le … \le p_{(m)}$$
(2)对于给定是统计显著性值$\alpha \in (0,1)$,找到最大的k,使得
$$p_{(k)} \le \frac{\alpha * k}{m}$$
(3)对于排序靠前的k个假设检验,认为它们是真阳性 (positive )
即:$reject \, H_0^{(i)},\, 1 \le i \le k$
$$
\begin{array}{c|l}
\hline
Gene & p-value \\
\hline
G1 & P1 =0.053 \\
\hline
G2 & P2 =0.001 \\
\hline
G3 & P3 =0.045 \\
\hline
G4 & P4 =0.03 \\
\hline
G5 & P5 =0.02 \\
\hline
G6 & P6 =0.01 \\
\hline
\end{array}
\, \Rightarrow \,
\begin{array}{c|l}
\hline
Gene & p-value \\
\hline
G2 & P(1) =0.001 \\
\hline
G6 & P(2) =0.01 \\
\hline
G5 & P(3) =0.02 \\
\hline
G4 & P(4) =0.03 \\
\hline
G3 & P(5) =0.045 \\
\hline
G1 & P(6) =0.053 \\
\hline
\end{array}
$$
$$\alpha = 0.05$$
$P(4) =0.03<0.05*\frac46=0.033$
$P(5) =0.045>0.05*\frac56=0.041$
因此最大的k为4,此时可以得出:在FDR<0.05的情况下,G2,G6,G5 和 G4 存在差异表达
可以计算出q-value:
$$p_{(k)} \le \frac{\alpha*k}{m} \, \Rightarrow \, \frac{p_{(k)}*m}{k} \le \alpha$$
| Gene | P | q-value |
|---|---|---|
| G2 | P(1) =0.001 | 0.006 |
| G6 | P(2) =0.01 | 0.03 |
| G5 | P(3) =0.02 | 0.04 |
| G4 | P(4) =0.03 | 0.045 |
| G3 | P(5) =0.045 | 0.054 |
| G1 | P(6) =0.053 | 0.053 |
根据q-valuea的计算公式,我们可以很明显地看出:
$$q^{(i)}=p_{(k)}^{(i)}*\frac{Total \, Gene \, Number}{rank(p^{(i)})}=p_{(k)}^{(i)}*\frac{m}{k}$$
即,根据该基因p值的排序对它进行放大,越靠前放大的比例越大,越靠后放大的比例越小,排序最靠后的基因的p值不放大,等于它本身
我们也可以从可视化的角度来看待这个问题:
对于给定的$\alpha \in (0,1)$,设函数$y=\frac{\alpha}{m}x \quad (x=1,2,…,m)$,画出这条线,另外对于每个基因,它在图上的坐标为$(rank(p_{(k)}^{(i)}),p_{(k)}^{(i)})=(k,p_{(k)}^{(i)})$,图如下:
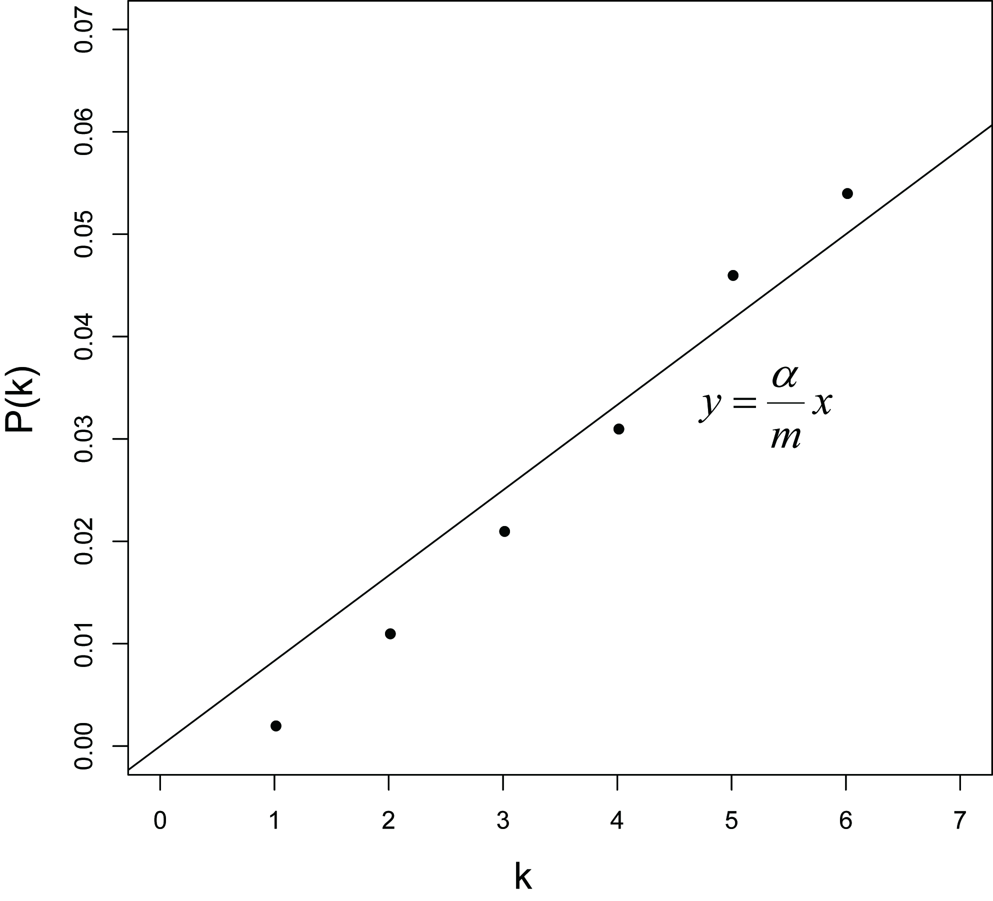
通过设置$\alpha$可以改变图中直线的斜率,$\alpha$越大,则直线的斜率越大,落在直线下方的点就越多,通过FDR检验的基因也就越多,反之,直线的斜率越小,落在直线下方的点就越少,通过FDR检验的基因也就越少
当固定$\alpha$,而统计检验次数m增加时,这条直线的斜率变小,落在直线下方的点就越少,通过FDR检验的基因也就越少
参考资料:
(1) Storey, J.D. & Tibshirani, R. Statistical signifcance for genomewide studies.Proc. Natl. Acad. Sci. USA 100, 9440–9445 (2003)
(2) 国科大研究生课程《生物信息学》,陈小伟《基因表达分析》




